Otimização Paramétrica de uma Asa
Na fase M1 desta unidade curricular foi alvo de estudo a parametrização de uma asa, no âmbito do projeto Automec UAV. Esta parametrização foi efetuada através de diferentes abordagens: por um lado, uma modelação paramétrica através da implementação de Design Tables e Macros, tal como a experimentação com um software de modelação algorítmica, o BeeGraphy. No entanto, embora os resultados obtidos tenham sido satisfatórios, sentiu-se a necessidade de uma otimização dos modelos de asas criados, de forma a poder obter uma maximização do seu desempenho.
Este desafio conduz-nos ao tema da presente fase M2: otimização. Foi escolhido como alvo de um estudo, como estudado anteriormente, uma asa e foi implementada um processo de otimização paramétrica. Assim, nesta fase, foi abordado um método que permite não só automatizar a modelação da asa já explorada anteriormente como também garantir que estas são funcionais, tendo em conta diversos parâmetros, e ainda avaliar qual a mais adequada.
Para isto foram diversos os passos seguidos, passos esses que serão explorados nesta página.
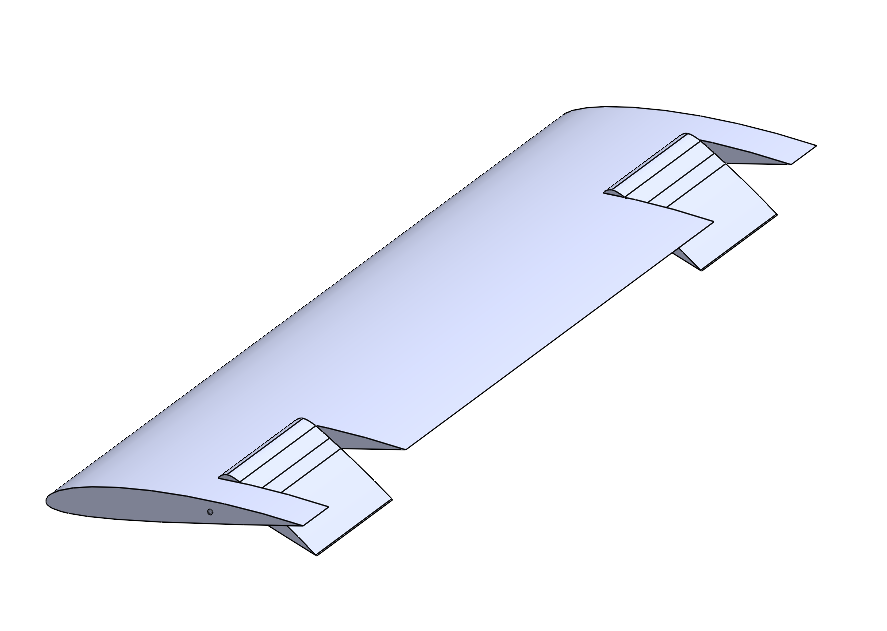
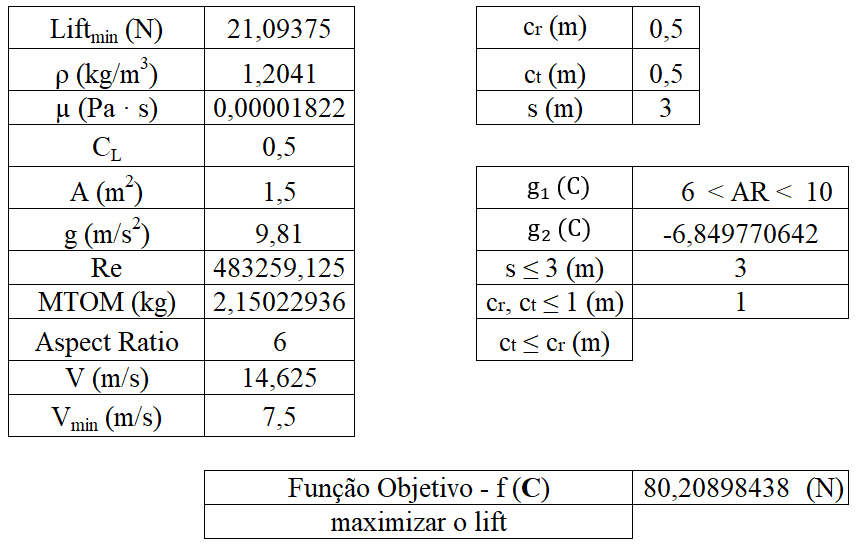
Compilação de informação
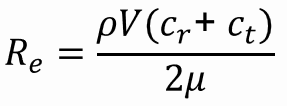
Número de Reynolds
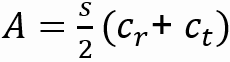
Área da asa
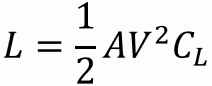
Força de sustentação
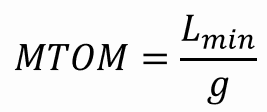
Maximum Takeoff Mass
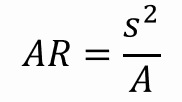
Aspect Ratio

Função Objetivo e Variáveis de Projeto
Como se sabe, um dos fatores mais importantes para que um drone voe é a força de sustentação gerada pela asa, pelo que se definiu a função objetivo maximizar a força de sustentação gerada, tendo como variáveis de projeto a corda da raiz, a corda da ponta e a envergadura da asa.
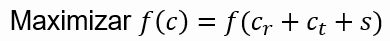
Utilizando as fórmulas reunidas na etapa de compilação de informação, chegou-se à seguinte função:
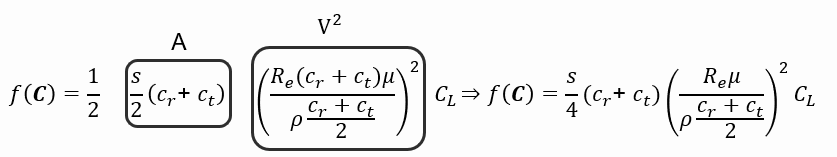
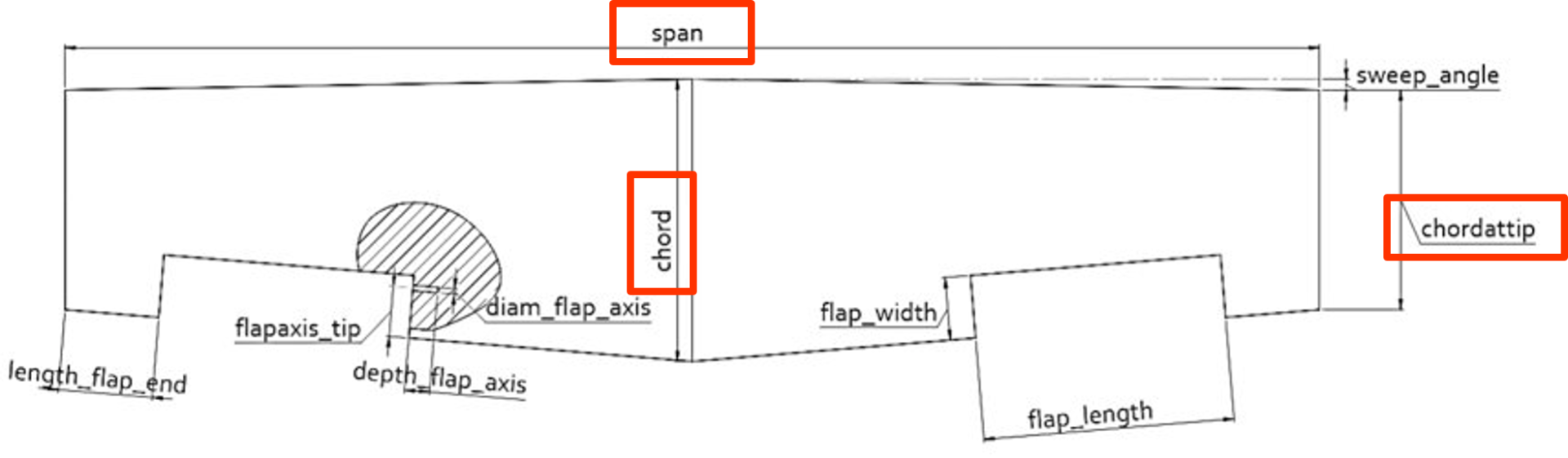
Restrições
Tendo em conta as restrições impostas pelo projeto para o qual a asa é desenvolvida, Automec UAV, nomeadamente quanto às dimensões máximas da asa, assim como as condições que têm de ser respeitadas para o bom funcionamento do drone, foram estabelecidas as seguintes restrições:
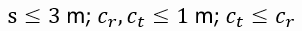
Domínio das variáveis de projeto:
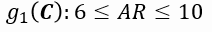
Limite estabelecido para o aspect ratio:
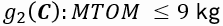
Limite mínimo de sustentação:
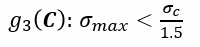
Limite de tensão máxima:
Otimização Black-Box
Na otimização black-box o objetivo e as restrições são tratadas como uma "caixa preta", o que leva à necessidade da utilização de um programa de otimização, de uma interface e de um programa externo.
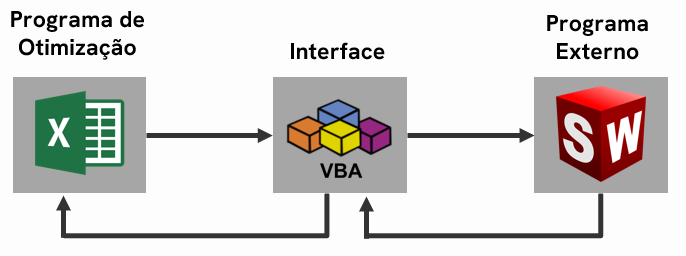
O objetivo final é, então....
Utilizar o Programa de Otimização solver do Excel para obter os valores das variáveis globais que maximizem a sustentação da asa, sendo que uma das restrições associadas incorpora dados retirados do Programa Externo SolidWorks.
Uma vez que nenhum dos elementos do grupo possuía experiência significativa a trabalhar com o VBA do Excel, e que seria precisamente essa a 'torre de controlo' do trabalho a desenvolver, por ser a ponte entre o Excel e o SolidWorks, o objetivo final foi dividido num conjunto de metas sucessivas. De modo que cada meta atingida com sucesso passasse a ser uma base sólida para a seguinte, sucessivamente até se obter o programa desejado. As metas em questão são as seguintes:
- Modelar autonomamente uma metade da asa total, com base nos valores das variáveis globais retirados das células correspondentes. Isto implicaria um fluxo de informação Excel -> VBA -> Solidworks
- Criar uma simulação estática na peça modelada, em que a sustentação gerada por essa asa (cujo valor é retirado da célula do Excel correspondente) é aplicado na face que corresponde à sua ponta. A face que corresponde à sua raiz é dada como fixa, e assume-se que o material é EPS.
Um dos principais desafios desta fase, e que pode, na sua essência, ser encarado como uma sub-fase, foi modificar o método de escolha utilizado pelo VBA de modo a que, mesmo alterando os valores das variáveis globais, continuassem a ser selecionadas as faces corretas para a aplicação de forças e fixações.
Extrair e manipular os dados resultantes da simulação realizada, o que acrescentaria um fluxo de informação no sentido Solidworks -> VBA
Aplicar os dados obtidos à restrição apropriada, em cada iteração realizada pelo solver, de modo a fechar o fluxo de informação com o acrescento do sentido VBA -> Excel
Devido ao facto de terem sido desenvolvidos vários códigos, e de cada código ser ainda relativamente extenso, para além do facto de, em certos aspetos, serem bastante repetitivos, em cada etapa somente serão apresentados os pontos que a distinguem da anterior. Serão também discutidos, ao longo das etapas e numa fase final, alguns pontos importantes / que se apresentaram difíceis de resolver. Espera-se que, caso um projeto semelhante venha a ser conduzido no futuro, estas considerações sirvam de base e/ou ajudem a resolver eventuais problemas que possam surgir.
Criação do Solver
Modelação da Peça
Existem diversas possibilidades no que respeita à aplicação do VBA para a modelação da asa. Por exemplo, o código desenvolvido tanto pode ser aplicado a uma peça já existente, como pode criar uma peça de raiz; e, de forma similar, pode assumir que o SolidWorks já se encontra aberto, ou que seja necessário abri-lo. Para facilitar a utilização do código desenvolvido por um utilizador exterior, partiu-se do princípio que a modelação da asa seria sempre realizada de raiz. Seria, assim, também necessário que o VBA tivesse a capacidade de iniciar a aplicação externa.
Algo a retirar desta experiência de programar em VBA é que, pelo menos no que refere a interações com o SolidWorks, o código é algo peculiar no que refere às suas variáveis e funções disponibilizadas (quando em comparação com as restantes linguagens de programação utilizadas anteriormente).
Em relação às variáveis a utilizar, é importante ter desde logo em conta qual o alcance que se pretende que as mesmas tenham. Isto é, se se pretende que sejam específicas a uma determinada função ou Subrotina (Sub), ou se se pretende que sejam visíveis a todos os procedimentos existentes dentro da folha de Excel em questão.
Em relação às funções, por sua vez, o seu nome é por norma bastante indicativo da tarefa que desempenham. Todavia, esta simplicidade é muitas vezes anulada pela complexidade dos parâmetros de entrada que lhe estão associados.
Estes são dois aspetos que vale a pena manter em mente ao longo durante todo o processo que se segue.
A atualização das bibliotecas ativas é a primeira etapa a realizar. Estas variam consoante a versão do SolidWorks existente no dispositivo, pelo que é difícil estabelecer uma lista concreta a utilizar. Devido a esta complicação, foram selecionadas todas as bibliotecas relacionadas com o SolidWorks. Nomeadamente, todas as bibliotecas começadas por 'sld', 'SOLIDWORKS' ou 'SolidWorks'. Foi ainda adicionada a biblioteca COSMOS Motion SolidWorks Type Library por estar associada à realização de simulações.
Dim OSw As SldWorks.SldWorks
Dim swModel As SldWorks.ModelDoc2
Dim swSketchMgr As SldWorks.SketchManager
Dim swFeatMgr As SldWorks.FeatureManager
Dim swPlane As SldWorks.RefPlane
Dim Part As Object
Dim boolstatus As Boolean
Dim longstatus As Long, longwarnings As Long
Dim swFeature As Object
Dim swSketch As SldWorks.Sketch
Dim chordroot As Double, chordtip As Double, envergadura As Double
Dim x As Double, y As Double, z As Double
A declaração das variáveis ocupa a primeira parte do código. Apesar se não ser estritamente necessário declarar todas as variáveis nesta etapa, caso todas as variáveis estejam reunidas neste grupo, é bastante mais fácil alterar o seu tipo caso seja, posteriormente, necessário.
Tendo em consideração que nesta etapa ainda não é necessário criar vários processos distintos, basta usar um 'Dim' para a inicialização das variáveis.
A inicialização do Solidworks, em si, resume-se às linhas
Set OSw = CreateObject("sldworks.Application")
OSw.Visible = True
Ao passo que a criação de um novo documento, assim como a sua ativação, são realizadas em
Set swModel = OSw.NewDocument("C:\ProgramData\SolidWorks\SOLIDWORKS 2024\templates\Part.prtdot", 0, 0, 0)
Set Part = OSw.ActiveDoc
Em seguida, a extração dos valores das variáveis globais a partir das células do Excel com recurso à função Range é realizada em
chordroot_m = Range("F5").Value
chordroot = chordroot_m * 1000
chordtip_m = Range("F6").Value
chordtip = chordtip_m * 1000
envergadura = Range("F7").Value
É de ressaltar que, devido à forma como os pontos de referência para o airfoil são definidos, é necessário transformar os valores das duas chords em milímetros.
Com ambas as chords e a envergadura definidas, o passo seguinte passa por desenhar as curvas dos airfoils da raiz e da ponta. No primeiro, o airfoil da raiz, a chordroot é utilizada para dimensionar os pontos retirados do website Airfoil Tools. Cada um dos mesmos é dividido nas suas três coordenadas, que por sua vez são multiplicadas pela variável em questão, tal como se pode observar em
Part.InsertCurveFileBegin
x = 0.001 * chordroot: y = 0 * chordroot: z = 0 * chordroot
boolstatus = Part.InsertCurveFilePoint(x, y, z)
Após a introdução de todos os pontos, um novo sketch é criado, no plano frontal. A curva definida é então convertida numa entidade de sketch.
' Create a new sketch on the Front Plane
boolstatus = Part.Extension.SelectByID2("Front Plane", "PLANE", 0, 0, 0, False, 0, Nothing, 0)
Part.SketchManager.InsertSketch True
' Convert each curve to a sketch entity
boolstatus = Part.Extension.SelectByID2("Curve1", "REFERENCECURVES", 0, 0, 0, False, 0, Nothing, 0)
boolstatus = Part.Extension.SelectByID2("Curve2", "REFERENCECURVES", 0, 0, 0, True, 0, Nothing, 0)
Part.SketchManager.SketchUseEdge3 False, False ' Convert curves to sketch entities
' Exit sketch
Part.SketchManager.InsertSketch False
O processo é então repetido para o airfoil da ponta. Neste caso, é necessária a utilização tanto da chordtip como da envergadura, uma vez que para além de dimensionar o airfoil em si, é necessário aplicar uma translação ao mesmo. A qual é conseguida, precisamente, pela envergadura.
Part.InsertCurveFileBegin
x = 0.001 * chordtip: y = 0 * chordtip: z = envergadura * 0.5
boolstatus = Part.InsertCurveFilePoint(x, y, z)
Finalmente, após a criação dos dois sketchs que contêm os airfoils das extremidades da meia asa, é somente necessário criar um loft para os unir, tal como é realizado em seguida. Para evitar possíveis complicações futuras, derivadas de alterações das curvas consideradas, são selecionados os sketch como um todo, ao invés das curvas em si, como referências para esta operação.
boolstatus = Part.Extension.SelectByID2("Sketch1", "SKETCH", 0, 0, 0, True, 0, Nothing, 0)
boolstatus = Part.Extension.SelectByID2("Sketch2", "SKETCH", 0, 0, 0, True, 0, Nothing, 0)
Part.ClearSelection2 True
boolstatus = Part.Extension.SelectByID2("Sketch1", "SKETCH", 0, 0, 0, False, 1, Nothing, 0)
boolstatus = Part.Extension.SelectByID2("Sketch2", "SKETCH", 0, 0, 3, True, 1, Nothing, 0)
Part.FeatureManager.InsertProtrusionBlend False, True, False, 1, 0, 0, 1, 1, True, True, False, 0, 0, 0, True, True, True
Aplicação de uma Simulação
Uma vez que o processo relacionado com a extração de resultados a partir da simulação se resume a um pequeno conjunto de linhas de código, a sua explicação será também ela incluída na presente etapa. Assim, e partindo do código desenvolvido na etapa anterior, a primeira etapa a realizar é a inicialização do Add-In de simulação. Tal como mencionado anteriormente, é preferível que a sua inicialização enquanto objeto seja feita na parte inicial do código, no entanto, é perfeitamente válido fazê-lo no meio do código.
' Initialize Simulation Add-in
Dim COSMOSWORKSObj As Object
Dim CWAddinCallBackObj As Object
Set CWAddinCallBackObj = OSw.GetAddInObject("SldWorks.Simulation")
Set COSMOSWORKSObj = CWAddinCallBackObj.COSMOSWORKS
Nas linhas acima, surge uma pequena contradição. As variáveis baseiam-se em 'CosmosWorks', todavia, ao abrir o Add-In é utilizada a numenclatura 'Simulation'. Na realidade, ambos os nomes correspondem à mesma coisa; a única diferença reside na versão do SolidWorks que está a ser utilizada. O 'CosmosWorks' é utilizado para versões antigas, enquanto que as versões mais recentes se referem a este Add-In como 'Simulation'. Esta é uma particularidade que pode facilmente conduzir a erros no projeto.
Isto não é necessário se o objetivo for exclusivamente o de modelar uma meia-asa.
Dim motionStudyMgr As Object
Set motionStudyMgr = Part.Extension.GetMotionStudyManager()
Dim ActiveDocObj As Object
Dim StudyManagerObj As Object
Dim LoadsAndRestraintsManagerObj As Object
Dim ErrorCodeObj As Long
Dim ContactManagerObj As Object
Set ActiveDocObj = COSMOSWORKSObj.ActiveDoc()
Set StudyManagerObj = ActiveDocObj.StudyManager()
StudyManagerObj.ActiveStudy = 0
Dim NewStudyName As String
NewStudyName = "Static 1"
Dim CWNewStudy As Object
Set CWNewStudy = StudyManagerObj.CreateNewStudy3(NewStudyName, 0, 0, ErrorCodeObj)
boolstatus = Part.Extension.SelectByID2("Loft1", "SOLIDBODY", 0, 0, 0, True, 0, Nothing, 0)
Dim StudyObj As Object
Set StudyObj = StudyManagerObj.GetStudy(0)
Dim SolidManagerObj As Object
Set SolidManagerObj = StudyObj.SolidManager()
ErrorCodeObj = SolidManagerObj.SetLibraryMaterialToSelectedEntities("custom materials", "E.P.S.")
Part.ClearSelection2 True
Para a realização de simulações autonomamente, são necessárias várias variáveis adicionais, direcionadas à aplicação de estudos.
Aqui, é atribuído um nome ao estudo a realizar, que é aplicado ao objeto resultante da operação de loft efetuada anteriormente.
O material utilizado na asa, E.P.S., não faz parte da base de dados do SolidWorks. Como tal, é necessária a criação prévia de um Custom Material que o represente. As informações usadas no mesmo foram retiradas do website MatWeb. A pasta em que o material criado se encontra, e o nome que lhe é atribuído, são os parâmetros necessários para a utilização da função SetLibraryMaterialToSelectedEntities()
Definido o material, é então necessário selecionar a face à qual será aplicada a fixação, neste caso, a face correspondente à raiz. Uma particularidade do VBA com SolidWorks é, precisamente, a forma como as faces são selecionadas. Neste contexto, tipicamente recorre-se à função SelectByRay que, essencialmente, seleciona a primeira entidade intersetada pelo raio que define. Este raio tem origem num ponto, cujas coordenadas são definidas pelos três primeiros argumentos da função, apresenta um determinado vetor de direção, definido pelos três seguintes argumentos, e é delimitado por um raio. É ainda necessário introduzir o tipo de entidade que se pretende selecionar, a ação a realizar caso a entidade já se encontre na lista de entidades selecionadas, o valor a usar como marca e o tipo de opção de seleção. Inicialmente, estes foram os parâmetros de seleção:
boolstatus = Part.Extension.SelectByRay(0.241406838526359, 1.59297978658799E-02, 0, -0.631634233055523, -0.18531998030324, 0.752791272885631, 8.13551995470029E-03, 2, True, 0, 0)
Todavia, após uma tentativa de alteração dos valores das variáveis globais, rapidamente se notou que este conjunto de valores não era apropriado para a maioria dos casos. Como tal, e com base nas informações expostas anteriormente, introduziu-se a seguinte modificação:
Dim x_origin As Double
Dim y_origin As Double
x_origin = (chordroot * 0.001) / 2
y_origin = (chordroot * 0.00009974) / 2' Redraw
boolstatus = Part.Extension.SelectByRay(x_origin, y_origin, 0, -0.631634233055523, -0.18531998030324, 0.752791272885631, 8.13551995470029E-03, 2, True, 0, 0)
Em que as variáveis x_origin e y_origin são ajustadas de modo a que o ponto inicial do raio se localize o mais próximo possível do centro do airfoil de forma automática. Um processo similar é realizado aquando da escolha da face da ponta para a aplicação da força.
Set CWForceObj = LoadsAndRestraintsManagerObj.AddForce3(0, 0, 0, 0, 0, 0, (DistanceValues), (ForceValues), 0, False, 0, 0, 4, 1, (ComponentValues), False, False, (DispArray), ReferenceGeometryDispatchObj2, False, ErrorCodeObj)
Aplicação da força essa cuja codificação representou um desafio. Esta é uma força que atua na face do airfoil da ponta, apresentando uma direção vertical, e com uma intensidade derivada da sustentação previamente calculada. A sua aplicação é realizada por meio de uma função que apresenta um total de vinte e um argumentos. Inicialmente, começou-se por usar a formulação automaticamente gerada na gravação de um macro no SolidWorks. Todavia, esta formulação levava a erros sucessivos. Além disso, conforme se procurou experimentar o macro gerado pelo próprio SolidWorks sobre um modelo de asa gerado com o código da etapa anterior, este também não funcionava corretamente.
Seguiu-se, então, uma etapa de debug em que se procurou validar todos os processos de seleção prévios à implementação desta função, para garantir que o problema era da função em si, e não do facto de se estar a tentar aplicar uma força sobre algo inexistente. Confirmado que o problema se encontrava, de facto, na função, realizaram-se várias modificações dos seus argumentos, com base em dados retirados do website SolidWorks API Help. Infelizmente, nenhuma das modificações conduziu a resultados favoráveis.
O problema?
Um dos argumentos em questão serve para especificar o tipo de geometria que vai servir de referência para definir a direção da força a aplicar. Até ao momento, a geometria em questão (que durante a gravação do macro é selecionada pelo utilizador) consistia de uma linha vertical desenhada no mesmo plano que a face em que é aplicada a força. Todavia, este argumento somente suporta três tipos de geometrias: arestas, eixos e faces/planos. Ou seja, a linha que estava a ser usada não se enquadrava em nenhuma das categorias.
Retornou-se então um pouco atrás, à parte da modelação, e modificou-se o código de modo a converter a linha em questão num eixo. Após esta ação, a função deixou de dar erro.
Aplicada a força, a definição da malha a utilizar e o comando para correr a simulação são efetuados em:
Dim MeshObj As Object
Set MeshObj = StudyObj.Mesh()
MeshObj.Quality = 1
MeshObj.UseJacobianCheckForSolids = 2
MeshObj.MesherType = 2
MeshObj.MinElementsInCircle = 8
MeshObj.GrowthRatio = 1.4
MeshObj.SaveSettingsWithoutMeshing = False
MeshObj.Unit = 0
ErrorCodeObj = StudyObj.CreateMesh(0, 40, 2)
ErrorCodeObj = StudyObj.RunAnalysis()
Finalmente, a extração da tensão máxima a que a asa está sujeita é realizada com:
Dim Stress As Variant
Stress = ResultsObj.GetMinMaxStress(9, 0, 1, Nothing, 3, ErrorCodeObj)
Na realidade, são quatro os valores que a função acima retorna: o nó que experiencia a mínima tensão, assim como a tensão em causa, e o nó em que se manifesta o maior valor de tensão, assim como a tensão associada. Como tal, o valor que se pretende obter corresponde ao último item do array Stress.
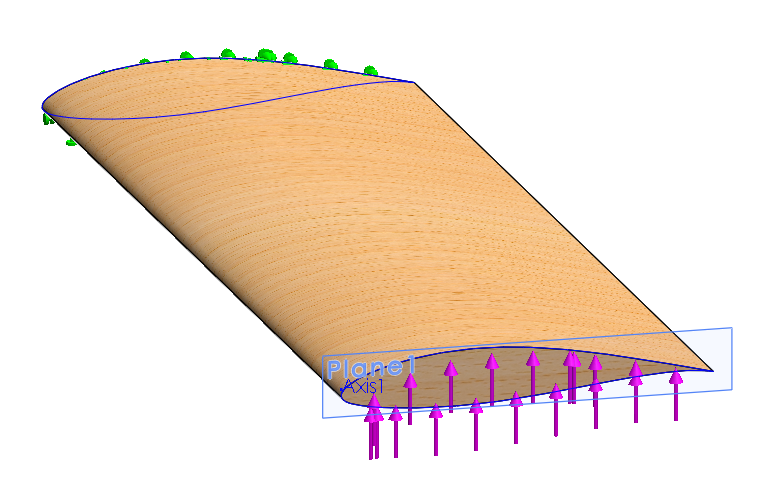
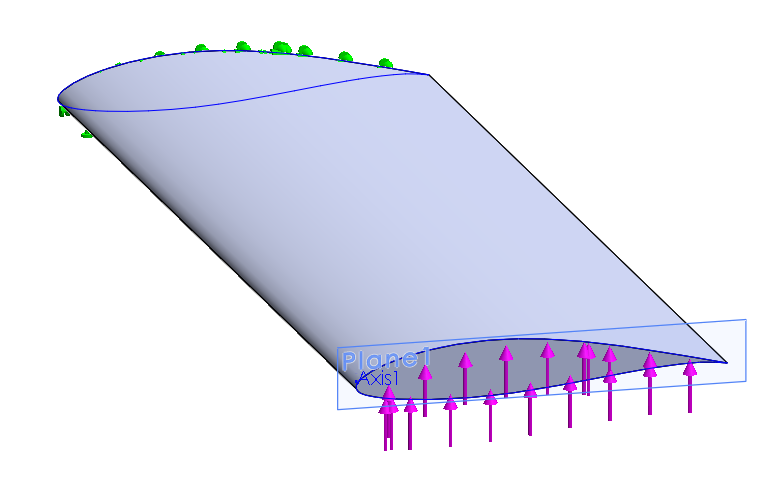
Comparação de Materiais
De modo a simular o processo iterativo realizado pelo solver, mas com um nível de complexidade melhor, desenvolveu-se uma Subrotina responsável por comparar as tensões sofridas, para uma mesma asa, para três materiais diferentes. Para isso, as tensões de cedência dos três materiais - balsa, E.P.S. e PE de baixa densidade - foram introduzidas no Sub. Este é então responsável por, para cada um dos materiais em questão, chamar a rotina que tem vindo a ser explorada em ambas as etapas anteriores, retirar os valores das tensões máximas e comparar qual é o caso que apresenta um maior fator de segurança.
Evolutionary Solver
Concluídas as etapas anteriores, procurou-se incorporar o código desenvolvido no Solver anteriormente criado. Todavia, das pesquisas efetuadas não se retirou nenhuma conclusão óbvia sobre como o fazer. Deste modo, uma alternativa que se procurou implementar para obter um resultado similar, foi a criação de um código que implementasse, por si próprio, um algoritmo de otimização. O fluxo de dados final seria, obviamente, ligeiramente alterado, limitando a duas o número de interações entre o Excel e o VBA (uma primeira vez para extrair os valores das variáveis globais, e uma segunda para os substituir com os valores otimizados).
O algoritmo que se procurou implementar foi do tipo evolucionário. Este pode, na sua essência, ser resumido de acordo com o seguinte diagrama:
Com base nisto, foi então criado um novo Sub, juntamente com um conjunto de funções, que podem ser encontradas em:
Porém, este código não se encontra completo! Ao tentar implementá-lo, durante a fase de testes, rapidamente se encontrou um loop que produzia sempre os mesmos resultados ao longo das sucessivas gerações - por outras palavras, nenhuma operação de otimização chegava de facto a ser realizada. Devido a limitações de tempo, não chegou a ser possível resolver este problema. Assim, os códigos disponibilizados na página acima são meramente ilustrativos.
Com base ainda neste algoritmo, criou-se um novo código onde se procurou forçar a otimização numa só geração. Ou seja, ao invés de introduzir mutações e crossovers ao longo de sucessivas gerações, aumentou-se a população da primeira e única geração e comparou-se os resultados obtidos, de modo a o próprio código identificar a solução que gera a maior sustentação. Os resultados obtidos não serão, obviamente, tão otimizados como seriam caso o algoritmo acima fosse implementado com sucesso. Ainda assim, permitem incorporar todas as etapas visadas até agora com sucesso.
Incorporação no Solver do Excel
Com base nos materiais disponibilizados pelo docente após a apresentação final, foi realizada uma restruturação do solver que fora antes aplicado, assim como dos códigos do VBA envolvidos, produzindo assim um sistema incorporado diretamente no solver do Excel, tal como era o objetivo inicial.
Para tal, o VBA foi utilizado para criar quatro funções diferentes, todas elas tendo os valores das três variáveis de projeto como argumento:
- FuncOpt - a função que se pretende otimizar. Esta devolve a sustentação gerada tendo por base os valores introduzidos nos seus argumentos;
Function FuncOpt(indchordroot, indchordtip, indenvergadura) As Double
Dim Reynolds As Double
Dim CL As Double
Dim density As Double
Dim miu As Double
Dim lifttemp As Double
Reynolds = Range("C10").Value
miu = Range("C5").Value
density = Range("C4").Value
CL = Range("C6").Value
lifttemp = (indenvergadura / 4) * (indchordroot + indchordtip) * ((Reynolds * miu) / (density * (indchordroot + indchordtip) / 2)) ^ 2 * CL
Debug.Print liftemp
FuncOpt = lifttemp
End Function
- A_R - a função de restrição associada ao Aspect Ratio, que devolve o seu valor, tendo por base os valores introduzidos nos seus argumentos;
Function A_R(indchordroot, indchordtip, indenvergadura) As Double
Dim Area As Double
Dim ar As Double
Area = (indenvergadura / 2) * (indchordroot + indchordtip)
ar = (indenvergadura * indenvergadura) / Area
A_R = ar
End Function
- mtom - a função de restrição associada ao Maximum Take-Off Mass. Esta devolve o valor calculado, mediante os valores inseridos;
Function mtom(indchordroot, indchordtip, indenvergadura) As Double
Dim liftmin As Double
Dim Vmin As Double
Dim CL As Double
Dim Area As Double
Dim MTOM_ As Double
Dim gravity As Double
Area = (indenvergadura / 2) * (indchordroot + indchordtip)
Vmin = Range("C9").Value
CL = Range("C6").Value
gravity = Range("C7").Value
liftmin = 0.5 * Area * (Vmin * Vmin) * CL
MTOM_ = liftmin / gravity
mtom = MTOM_
End Function
- maxt - a função de restrição associada à tensão de cedência. Esta começa por calcular a sustentação gerada com base nos valores introduzidos nos seus argumentos. Em seguida, abre o SolidWorks, modela a asa consoante esses mesmos valores e aplica-lhe a força correspondente, calculada previamente. Em seguida, extrai os dados relativos à tensão máxima experenciada pela peça.
Function maxt(indchordroot, indchordtip, indenvergadura)
Dim Reynolds As Double
Dim CL As Double
Dim density As Double
Dim miu As Double
Dim MaxStress As Double
Dim lifttemp As Double
Reynolds = Range("C10").Value
miu = Range("C5").Value
density = Range("C4").Value
CL = Range("C6").Value
lifttemp = (indenvergadura / 4) * (indchordroot + indchordtip) * ((Reynolds * miu) / (density * (indchordroot + indchordtip) / 2)) ^ 2 * CL
tempchordroot = indchordroot
tempchordtip = indchordtip
tempenvergadura = indenvergadura
indlift = lifttemp
Call opensolidworkswithsolver
MaxStress = StressArray(3)
maxt = MaxStress
End Function
Estas funções são utilizadas nas células do Excel correspondentes, ao invés de, tal como acontecia anteriormente, as expressões serem escritas diretamente nas células em questão.
A Subrotina opensolidworkswithsolver (quarta linha a contar do fim, na função maxt) pode ser encontrada aqui.
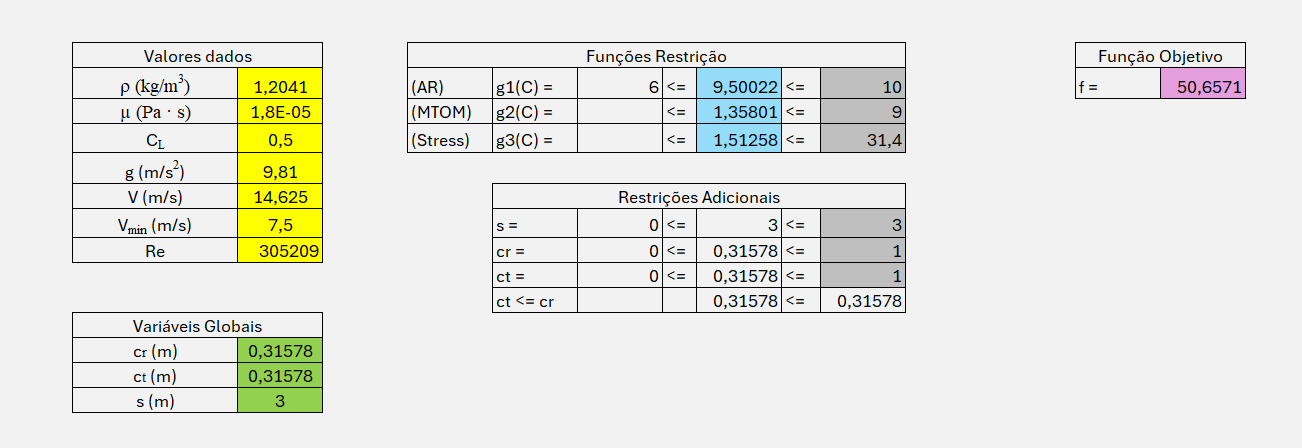
Novo Solver
Neste novo solver, são implementadas as três funções de restrição nas células a azul, ao passo que a função objetivo é implementada na célula a roxo.No vídeo seguinte, é possível observar um teste realizado à folha do Excel em que são implementadas as funções criadas. Neste, é alterado um dos valores das variáveis globais, o que, por sua vez, desencadeia uma alteração dos valores das células que são controladas pelas funções em questão. Apesar de o processo ser um pouco lento, o que não é tão notório devido ao facto de o vídeo estar acelerado, os valores são alterados automaticamente. Comprova-se, assim, que as funções funcionam.
No vídeo seguinte, por sua vez, é testado o solver em si. O processo total até ser atingida a otimização demora perto de meia hora pelo que, para este teste, indicou-se ao solver que o mesmo deveria avisar o utilizador a cada iteração concluída. O teste que se pode observar no vídeo apresenta somente duas destas iterações.
Considerações Finais
O desenvolvimento de um processo de otimização em que o VBA funciona como uma interface fundamental entre o Excel e o SolidWorks revelou-se um projeto desafiante. Desde logo por nenhum dos elementos do grupo ter experiência com a linguagem de programação, e também à complexidade automaticamente inerente à mesma.
Ao longo de todo o processo, e mesmo com a divisão do mesmo em diversas etapas, foram vários os problemas encontrados. Na parte da modelação, não surgiram contratempos relevantes, todavia, na parte relacionada à simulação, estes foram abundantes. Os principais erros encontrados deveram-se às funções utilizadas, sobretudo aquando da aplicação da força e da extração dos dados relativos às tensões máximas experenciadas pelas peças. Também o método de seleção acarretou alguns problemas, tal como descrito anteriormente.
Algo que se notou recorrentemente ao longo do projeto foi a falta de informação disponível, maioritariamente no que refere à realização de simulações. A acrescentar à falta de informações, notou-se também uma certa discrepância entre as informações disponibilizadas e a forma correta de as aplicar - quer isto dizer que, apesar de existirem, por exemplo, alguns exemplos de implementação de funções, é necessário adaptá-los tendo em conta as bibliotecas consideradas.
Bibliotecas essas que também foram uma grande fonte de problemas. Ao partilhar os projetos do Excel entre diferentes dispositivos, muitas vezes acontece que as bibliotecas contempladas não se encontram disponíveis, e surgem como 'Missing'. Tal como referido anteriormente, não foi possível definir com clareza quais as bibliotecas que são, de facto, necessárias aos diferentes programas que se desenvolveram - tendo sido ativado um possível excesso de bibliotecas de modo a contornar esse facto. Todavia, esse excesso é, precisamente, o que em muitos casos conduz a erros.
Todavia, apesar das dificuldades encontradas ao longo do projeto, este revelou-se bastante interessante, permitindo desenvolver competências numa área sobre a qual nenhum dos elementos tinha muitos conhecimentos. Apesar da peça que consitui a base do projeto ser relativamente simples, considera-se que o trabalho desenvolvido a partir da mesma foi de encontro aos objetivos propostos na cadeira.
